Research Topics

Field-Theoretic Simulations

Our group has pioneered the development of a new class of computer simulation methods where the degrees of freedom are fluctuating fields, rather than atom or particle coordinates. The basis for these "Field-Theoretic Simulations" (FTS) is a statistical field theory model, which is generally derived from a conventional particle-based model by means of exact mathematical transformations, such as Hubbard-Stratonovich transforms.

The FTS method has a number of advantages relative to traditional simulation techniques for studying the equilibrium structure and thermodynamic properties of complex fluids and polymers. Most importantly and unlike particle-based simulations, the method becomes more efficient as the density of the system increases, or the polymers become longer. The FTS method is also particularly convenient for studying charged polymers ("polyelectrolytes") that are characterized by long-range Coulomb interactions. In the field-theoretic framework, the problems normally associated with simulating Coulomb systems are minimized.

More information about the FTS method can be found in the following review articles:

• "Field-Theoretic Computer Simulation Methods for Polymers and Complex Fluids," G.H.Fredrickson, V.Ganesan, and F. Drolet, Macromolecules 35, 16 (2002). Link
• "Computational Field Theory of Polymers: Opportunities and Challenges," G.H.Fredrickson, Soft Matter 2, 1329 (2007). Link
• "Recent Developments in Fully Fluctuating Field-Theoretic Simulations of Polymer Melts and Solutions," K.T.Delaney and G.H.Fredrickson, J. Phys. Chem. B, 120, 7615 (2016). Link
• "Field-Theoretic Simulations: An Emerging Tool for Probing Soft Material Assembly,” G. H. Fredrickson and K. T. Delaney, MRS Bulletin 43, 371 (2018). Link

See also the Oxford University Press monograph:

• The Equilibrium Theory of Inhomogeneous Polymers, G.H.Fredrickson (Oxford University Press, Oxford, 2006). Link
• Field-Theoretic Simulations in Soft Matter and Quantum Fluids, G.H. Fredrickson and K.T. Delaney (Oxford University Press, Oxford, 2023). Link

Foundations of the FTS Method

While the FTS method is a standard research tool for many projects in the Fredrickson group, we have a number of ongoing research programs that are aimed at providing an improved theoretical basis for the method, developing more robust or efficient numerical methods for implementation, or extending the capabilities of FTS.

One branch of our research involves developing methods for systematic numerical "coarse-graining" of field theory models. The idea is to conduct a very fine-grained (i.e. high spatial resolution of the fields) FTS simulation on a small system and use the results to parameterize a new model on a coarser computational grid. That new model can then be simulated to study a larger system and further reparameterize an even coarser lattice field theory model. In this way, we can bootstrap a series of simulations that will cover a broad spectrum (6 decades or more) of spatial scales, while requiring only the parameters of the finest scale model as input. This type of multi-scale simulation technique is of considerable value in a variety of polymer and complex fluid formulation problems, including systems such as blends, emulsions, and polyelectrolyte complexes, where structure can extend from nanometer to millimeter length scales.

Another thrust in the group uses alternative field theory representations, such as the "coherent states" (CS) framework of quantum field theory, that can be applied to classical polymers and adapted for efficient numerical simulations. Such representations are particularly powerful for dealing with systems of reacting polymers, where the framework can automatically generate complex mixtures of reaction products based on rules encoded in the theory. As discussed in a later section, we have also recently shown that our FTS algorithms can be adapted to CS field theories of strongly correlated Bose quantum fluids.

Some publications in the FTS Foundations area include:

• "Free Energy Evaluation in Field-Theoretic Polymer Simulations," E.M.Lennon, K.Katsov, and G.H.Fredrickson, Phys. Rev. Lett. 101, 138302 (2008). Link
• "Numerical Coarse-Graining of Fluid Field Theories," M.C.Villet and G.H.Fredrickson, J. Chem. Phys. 132, 034109 (2010). Link
• "Field Theoretic Simulations in the Gibbs Ensemble," R.A.Riggleman and G.H.Fredrickson, J. Chem. Phys 132, 024104 (2010). Link
• "Polymer Field Theory Simulations on Graphics Processing Units," K.T.Delaney and G.H.Fredrickson, Computer Physics Communications 184(9), 2102 (2013). Link
• "Coherent States Formulation of Polymer Field Theory," X.Man, K.T.Delaney, M.C.Villet, H.Orland, and G.H.Fredrickson, J. Chem. Phys. 140, 024905 (2014). Link
• "Efficient Field-Theoretic Simulation of Polymer Solutions," M.C.Villet and G. H. Fredrickson, J. Chem. Phys. 141, 224115 (2014). Link
• "A Multi-Species Exchange Model for Fully Fluctuating Polymer Field Theory Simulations," D. Duechs, K. T. Delaney, and G. H. Fredrickson, J. Chem. Phys. 141, 174103 (2014). Link
• "Coherent States Field Theory in Supramolecular Polymer Physics," G. H. Fredrickson and K. T. Delaney, J. Chem. Phys. 148, 204904 (2018). Link
• "Optimized Phase Field Model for Diblock Copolymer Melts," J. V. Liu, C. J. Garcia-Cervera, K. T. Delaney, and G. H. Fredrickson, Macromolecules 52, 2878-2888 (2019). Link
• "Linear Scaling Self-Consistent Field Theory with Spectral Contour Accuracy," D. L. Vigil, C. Garcia-Cervera, K. T. Delaney, and G. H. Fredrickson, ACS Macro Letts., 8, 1402-1406 (2019). Link
• "Quantitative Comparison of Field Update Algorithms for Polymer SCFT and FTS," D. L. Vigil, K. T. Delaney, and G. H. Fredrickson, Macromolecules 54, 9804-9814 (2021). Link
• "Direct free energy evaluation of classical and quantum many-body systems via field-theoretic simulation" G.H. Fredrickson and K.T. Delaney, Proc. Natl. Acad. Sci. 119, 18 (2022). Link

Conformational Asymmetry and Architecture Effects in Block Polymers

During the last few decades block copolymers have received extensive research attention due to their ability to microphase separate into well-defined nanostructures that impart an array of different materials properties. However, nanostructures that can be stabilized in block copolymer systems have until recently been limited to a relatively small set. In recent years, conformational asymmetry and architectural variations within several classes of block copolymer systems have been found to facilitate the stabilization of a wide variety of topologically close-packed sphere phases known as Frank-Kasper phases. A particular focus of the Fredrickson group is the use of self-consistent field theory (SCFT) and FTS simulations to strengthen our fundamental understanding of the self-assembly behaviors of block copolymers with conformational asymmetry and/or new or emerging architectures (e.g., bottlebrush, comb, sequence-defined, and miktoarm stars) and to identify novel copolymer mesophases that are technologically relevant. This effort is in collaboration with experimental groups at UCSB, specifically the Bates, Segalman, and Hawker groups.

Supramolecular Polymers

An emerging theme in polymer science relates to the use of specific and reversible interactions to introduce unique structure, dynamics, and function in polymeric materials. This subject reflects a marriage of the rapidly emerging field of supramolecular chemistry with traditional polymer science. Examples of the supramolecular interactions that can be employed include hydrogen bonds, metal-ligand interactions, and pi-pi stacking. By attaching such moieties to polymer chains and adjusting the strength of the reversible binding, it is possible to achieve remarkable combinations of properties. For example, one can design adhesives and coatings that are fully bonded at low temperatures and are therefore mechanically robust, i.e. strong and tough, while at elevated temperatures the bonds break -- enabling easy flow and coating of a substrate.

Our group's research is focused primarily on the largely unexplored field of heterogeneous supramolecular polymers, where dissimilar polymers are linked by reversible bonds, thereby creating complex ensembles of block and graft copolymers, as well as inhomogeneous networks and gels. The interplay between the chemical equilibria of reversible binding and physical phase separation and microphase separation processes in such systems can produce a rich and diverse range of materials with widely varying properties and potential applications. Our approach in this field has been to define some simple models that serve to illustrate this interplay and analyze the models using a combination of analytical methods and FTS and SCFT simulations.

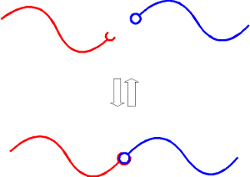
One example of such a model is a "supramolecular diblock" model in which two homopolymers, each bearing a complementary binding group at one end, are blended together. As shown below, the product of the reversible binding reaction is a diblock copolymer. We have mapped out the phase diagram of this seemingly simple system and have found a fascinating range of phase behaviors that can be driven thermally, or with blend composition, molecular weights, or binding equilibrium constant.

Recent group publications in the area of supramolecular polymers include:

• "Supramolecular Diblock Copolymers: A Field-Theoretic Model and Mean-Field Solution," E.H.Feng, W.B.Lee, and G.H.Fredrickson, Macromolecules 40, 693 (2007). Link
• "Phase Morphologies in Reversibly Bonding Supramolecular Triblock Copolymer Blends," W.B.Lee, R.Elliott, K.Katsov, and G.H.Fredrickson, Macromolecules 40, 8445 (2007). Link
• "Supramolecular Assembly in Telechelic Polymer Blends," R.Elliott and G.H.Fredrickson, J. Chem. Phys. 131, 144906 (2009). Link
• "Field-Theoretic Model of Inhomogeneous Supramolecular Polymer Networks and Gels," A. Mohan, R. Elliott, and G. H. Fredrickson, J. Chem. Phys. 133, 174903 (2010). Link
• "Macro- and Microphase Separation in Multifunctional Supramolecular Polymer Networks," Z. Mester, A. Mohan, and G. H. Fredrickson, Macromolecules 44, 9411 (2011). Link
• "Phase Coexistence of Reversibly Bonded Block Copolymers: A Unit Cell Gibbs Ensemble Approach," Z. Mester, N. A. Lynd, K. T. Delaney, and G. H. Fredrickson, Macromolecules 47, 1865-1874 (2014). Link

Polyelectrolyte Complexation

Another active research area in the Fredrickson group relates to the complexation of oppositely charged polyelectrolytes in aqueous solution. Due to electrostatic attractions and the entropy of counterion release, mixtures of polycations and polyanions in water tend to phase separate into a dense phase comprising most of the polymer and a dilute "supernatant" phase containing just small ions and water. The dense phase can be a solid precipitate, but in more interesting cases can itself be a hydrated fluid phase -- a so-called "complex coacervate" Such fluid polyelectrolyte complexes are pervasive in biology, but are also utilized in a variety of food and drug encapsulation technologies, as the coacervate phase will spread easily on many surfaces and has an ultralow interfacial tension against water. An interesting biological example, which is being intensively studied by the Waite group at UCSB, is the marine "sandcastle worm" who creates its underwater habitat by means of a protein-derived coacervate glue.

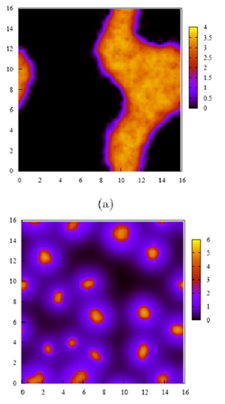
The Fredrickson group is engaged in collaboration with experimentalists in the Waite, Hawker, and Hahn groups to understand the fundamental chemistry and physics of a broad range of polyelectrolyte complexation phenomena. We are using analytical theories and FTS simulations to explore a variety of systems and physical mechanisms, including the role of molecular weight asymmetries and stoichiometric imbalances in the polyelectrolyte components of the mixtures and counter-ion partitioning between the supernatant and coacervate phases. We are also investigating the principles of self-assembly in "inhomogeneous coacervates" produced by complexing oppositely charged block copolymers, as well as developing theories of interfacial structure and thermodynamics in such systems.

Recent publications related to polyelectrolyte complexes include:

• "Field-Theoretic Simulation of Polyelectrolyte Complexation," Y.O.Popov, J.Lee, and G.H.Fredrickson, J. Polym. Sci. B: Polym. Phys. 45, 3223 (2007). Link
• "Complex Coacervation: A Field Theoretic Simulation Study of Polyelectrolyte Complexation," J.Lee, Y.O.Popov, and G.H.Fredrickson, J. Chem. Phys. 128, 224908 (2008). Link
• "Investigation of the Interfacial Tension of Complex Coacervates Using Field-Theoretic Simulations," R. A. Riggleman, R. Kumar, and G. H. Fredrickson, J. Chem. Phys. 136, 024903 (2012). Link

Quantum superfluids and liquid crystals

A new theme in our group is the application of numerical methods originally developed for polymers to simulate quantum field theories of interacting Bose Einstein condensates (BECs). The predominant computational tool in cold-atom physics is path integral Monte Carlo (PIMC), a particle-coordinate-based simulation method that builds on Feynman’s analogy between quantum particles and classical ring polymers. However, for large, dense systems at low temperatures the sampling process can become very expensive. On the other hand, field-based simulations inherently have favorable scaling with system density as compared to particle-based methods. We utilize a coherent states basis within a second-quantized, path integral framework that automatically embeds Bose statistics. Due to the complex nature of the coherent states fields, conferring a so-called “sign problem”, this theory cannot be sampled with standard Monte Carlo methods. However, we leverage algorithmic expertise in complex Langevin sampling developed over many years of simulating polymer field theories to tackle Bose quantum field theories. Our method is well-suited to study dense systems at low but finite temperatures where PIMC struggles and simplifying approximations are undesirable.

We currently use this method to study many kinds of quantum phenomena, targeting systems with a large number of particles (>1,000) and where the relevant model is plagued with a sign problem. BECs under mechanical rotation are one such system. When rotated in the laboratory, such BEC clouds exhibit arrays of “quantized vortices,” so-named because the vortex circulation is quantized. We are studying the structure and stability of these quantized vortices at various temperatures.

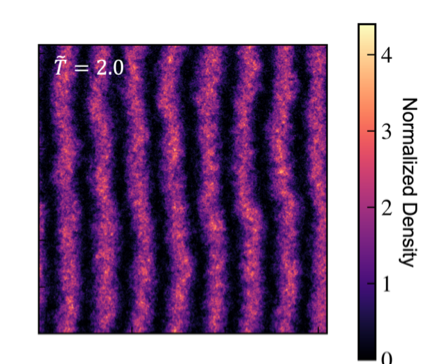
In addition, we are actively investigating the thermal phase transitions of spin-momentum coupled Bose-Einstein condensates, where superfluid smectic “stripe” liquid crystalline analogues are found. Field-theoretic simulations allow precise characterization of the low temperature stripe phase and its anisotropic superfluid character.

We also collaborate with experimentalists in David Weld’s atomic physics lab at UCSB to apply these simulations to real-world experiments. Since our method is well-suited for large systems at finite temperature, we are able to perform numerical experiments in complete 1:1 scale with the physical experiments, which helps in the interpretation and confirmation of experimentally observed phenomena.

Recent publications include:

• "Numerical simulation of finite-temperature field theory for interacting bosons” K.T. Delaney, H. Orland, G.H. Fredrickson. Physical Review Letters 124, 7, (2020). Link
• "Direct free energy evaluation of classical and quantum many-body systems via field-theoretic simulation” G.H. Fredrickson and K.T. Delaney, Proc. Natl. Acad. Sci. 119, 18 (2022). Link
• "Emergence of a Spin Microemulsion in Spin-Orbit Coupled Bose-Einstein Condensates,” E. C. McGarrigle, K. T. Delaney, L. Balents, and G. H. Fredrickson, preprint. Link
• "Thermodynamic Engine with a Quantum Degenerate Working Fluid,” E. Q. Simmons, R. Sajjad, K. Keithley, H. Mas, J. L. Tanlimco, E. Nolasco-Martinez, Y. Bai, G. H. Fredrickson, and D. M. Weld, preprint. Link

Dynamical simulations of polymer membrane formation processes

Block copolymers have attracted recent interest as candidate materials for ultrafiltration membranes, due to their ability to form isoporous integral-asymmetric membranes by the combined processes of self-assembly and nonsolvent-induced phase separation (SNIPS). The basic idea is to cast a block copolymer solution onto a substrate, evaporate the surface leading to self-assembly, and then immerse the film into a non-solvent bath. This process is highly non-equilibrium and requires accurate treatment of block copolymer thermodynamics, so we leverage our block copolymer field-theoretic models to provide the thermodynamic forces in a set of multicomponent diffusion transport equations. The numerical simulations are conducted with a dynamic version of self-consistent field theory (DSCFT) coupled to a stochastic thermal bath. We use this method to understand the effects of parameters such as solvent selectivity and film composition on the microstructure generated during the SNIPS process.

Recent publications include:

• "A Multi-Fluid Model for Microstructure Formation in Polymer Membranes,” D. R. Tree, K. T. Delaney, H. D. Ceniceros, T. Iwama, and G. H. Fredrickson, Soft Matter 13, 3013 (2017). Link
• "Mechanisms of Asymmetric Membrane Formation in Nonsolvent-Induced Phase Separation,” J. U. Garcia, T. Iwama, E. Y. Chan, D. R. Tree, K. T. Delaney, and G. H. Fredrickson, ACS Macro Lett. 9, 1617-1624 (2020). Link
• "Modeling Microstructure Formation in Block Copolymer Membranes Using Dynamical Self-Consistent Field Theory”, Douglas J. Grzetic, Anthony J. Cooper, Kris T. Delaney, and Glenn H. Fredrickson, ACS Macro Lett. 12 (1), 8-13 (2023). Link

Molecularly-informed field theory for formulation design

In collaboration with the Shell group at UCSB, we have developed a multiscale simulation workflow that connects the atomistic to the mesoscale, providing a powerful computational tool for the design of complex fluid formulations such as those used for personal care products, paints, coatings, and adhesives. This workflow uses relative entropy coarse-graining to convert representative atomic systems to fully parameterized field theory models that allow for direct access to free energies and rapid equilibration of macromolecular systems. The overall workflow leverages the efficiency of field theory in simulating large, dense, and high molecular weight systems, while providing chemical specificity through small-scale, all-atom simulations. Specifically, we derive parameters for the field theory by performing a systematic coarse-graining of representative all-atom simulations, using a strategy based on relative entropy minimization, and specifying coarse-grained interaction models that are amenable to an analytical field theory representation. This proposed simulation strategy enables efficient calculation of phase diagrams in the field representation while retaining chemical details via systematic coarse-graining of all-atom simulations.

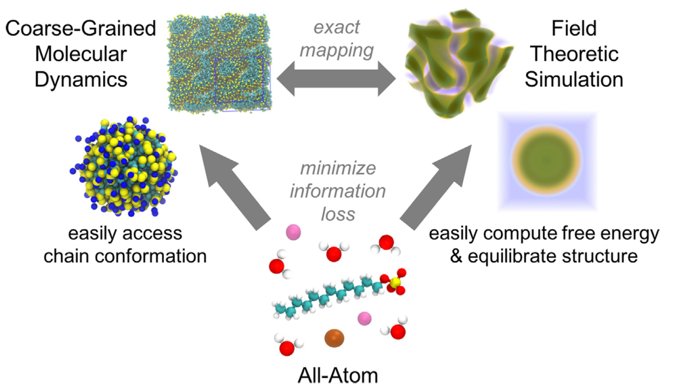
Recent publications include:

• "Molecularly informed field theories from bottom-up coarse-graining", N. Sherck, K. Shen, M. Nguyen, B. Yoo, S. Köhler, J. C. Speros, K. T. Delaney, M. S. Shell, and G. H. Fredrickson, ACS Macro. Lett. 10, 576 (2021). Link
• "Predicting Polyelectrolyte Coacervation from a Molecularly Informed Field-Theoretic Model", M. Nguyen, N. Sherck, K. Shen, C.E.R. Edwards, B. Yoo, S. Köhler, J.C. Speros, M.E. Helgeson, K.T. Delaney, M.S. Shell, and G. H. Fredrickson, Macromolecules. 55, 21, 9868–9879. (2022) Link
• "Predicting Surfactant Phase Behavior with a Molecularly Informed Field Theory.”, K. Shen, M. Nguyen, N. Sherck, B. Yoo, S. Köhler, J. C. Speros, K. T. Delaney, M. S. Shell, and G. H. Fredrickson. Journal of Colloid and Interface Science. (2023) Link

Solvent-free ion-containing polymers

Another recent theme within the Fredrickson group is the study of solvent-free polymer systems that have bound charged groups. Unlike traditional ionomers, we are focused on polymer systems with bulky pendant ions, such as those found in ionic liquids, which convey increased processability as well as ionic conductivity. Such materials are of keen interest in the field of energy storage, e.g. solid battery electrolytes and conductive binders, and in bioelectronic interfaces.

A class of systems of particular interest are blends of two polymer types, bearing opposite charges. Such a system is analogous to a complex coacervate, but without solvent. The backbone incompatibility of the polymers favors phase separation, but macroscopic phase separation is suppressed by the high electrostatic energy of charge separation. Fully homogeneous blends or microphases are obtained, the latter being readily tuned in symmetry and domain spacing with salt, temperature, or other external stimuli. Such “ionic compatibilization” is a powerful route to improving the miscibility of polymers, including difficult to process and alloy conjugated polymers, and could prove useful in the upcycling of plastic waste. We have developed a powerful “polarizable” field-theoretic framework for addressing such problems that allows permanent dipoles or induced dipoles to be included along with monopole charges in polymer side chains or backbones.

Another fascinating class of polymers have tethered bulky zwitterions (ZIs) that at sufficiently high loading crystallize within the polymer matrix. Recent experimental work in the Segalman lab at UCSB has shown that such materials are promising as solid polymer battery electrolytes (SPEs) with a fast “super-ionic” mode for Li ion transport that is decoupled from the backbone segmental dynamics. In collaboration with Dr. Amalie Frischknecht of Sandia National Laboratories, we are using atomistic molecular dynamics simulations to understand the detailed ion transport mechanism through or around the crystals by building models of both small molecule ZIs and their polyzwitterionic counterparts. It is hoped that this computational study will shed light on how to further improve the conductivity and selectivity of SPEs.

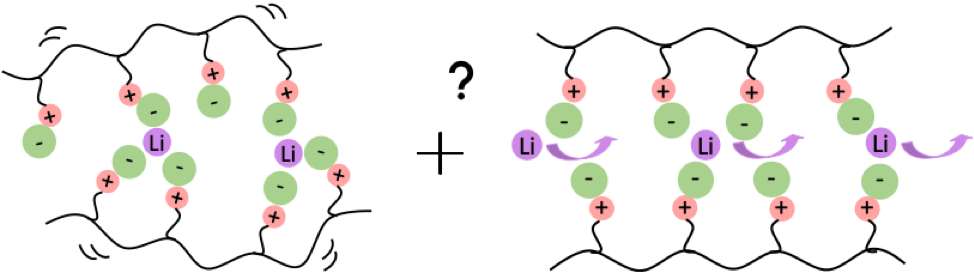
Recent publications in the area include:

• "Statistical Field Theory Description of Inhomogeneous Polarizable Soft Matter,” J. M. Martin, W. Li, K. T. Delaney, and G. H. Fredrickson, J. Chem. Phys. 145, 154104 (2016). Link
• "The Effective Chi Parameter in Polarizable Polymeric Systems: One-Loop Perturbation Theory and Field-Theoretic Simulations,” D. J. Grzetic, K. T. Delaney, and G. H. Fredrickson, J. Chem. Phys. 148, 204903 (2018). Link
• "The Role of Backbone Polarity on Aggregation and Conduction of Ions in Polymer Electrolytes,” N. S. Schauser, D. J. Grzetic, T. Tabassum, G. A. Kliegle, M. L. Le, E. M. Susca, S. Antoine, T. Keller, K. T. Delaney, S. Han, R. Seshadri, G. H. Fredrickson, and R. A. Segalman, J. Am. Chem. Soc., 142, 7055-7065 (2020). Link
• "Electrostatic Manipulation of Phase Behavior in Immiscible Charged Polymer Blends,” D. J. Grzetic, K. T. Delaney, and G. H. Fredrickson, Macromolecules 54, 2604-2616 (2021). Link
• "Design of Polymeric Zwitterionic Solid Electrolytes with Superionic Lithium Transport,” S. D. Jones, H. Nguyen, P. M. Richardson, Y.-Q. Chen, K. E. Wyckoff, C. J. Hawker, R. J. Clément, G. H. Fredrickson, and R. A. Segalman, ACS Central Science 8, 169-175 (2022). Link
• "Ionic Compatibilization of Polymers,” G. H. Fredrickson, S. Xie, L. Le, D. Sun, D. J. Grzetic, D. L. Vigil, M. L. Chabinyc, and R. A. Segalman, ACS Polymers Au, 2, 299-312 (2022) [perspective]. Link
• "Decoupling of Ion Transport and Matrix Dynamics to Make High Performance Solid Polymer Electrolytes,” S. D. Jones, J. Bamford, G. H. Fredrickson, and R. A. Segalman, ACS Polymers Au, 2, 430-448 (2022) [perspective]. Link
• "Electrostatic Interactions Control the Nanostructure of Conjugated Polyelectrolyte-Polymeric Ionic Liquid Blends,” M. L. Le, D. Grzetic, K. T. Delaney, K.-C. Yang, S. Xie, G. H. Fredrickson, M. Chabinyc, and R. A. Segalman, Macromolecules 55, 8321-8331 (2022). Link
• "Compatibilization of Polymer Blends by Ionic Bonding,” S. Xie, K. Karnaukh, K.-C. Yang, D. Sun, K. T. Delaney, J. Read de Alaniz, G. H. Fredrickson, and R. A. Segalman, Macromolecules 56 (10), 3617-3630 (2023). Link